Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

19.2: Diffraction Patterns

Last updated

Aug 24, 2023
Save as PDF
- 19.1: Introduction
- 19.3: Two-dimensional Diffraction

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

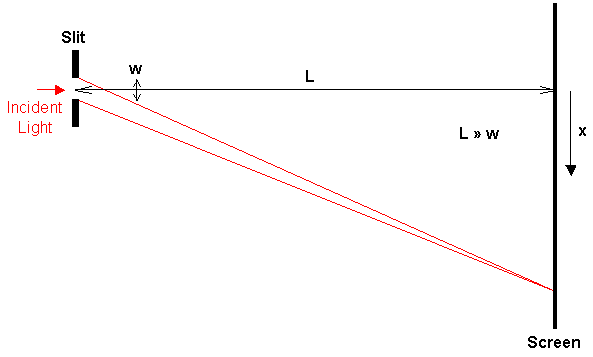
$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Laser diffraction experiments can be conducted using an optical bench, as shown below. Light from the laser (of wavelength λ) is diffracted by a mask (usually a small aperture or grating) and projected onto the screen, located at a large distance away, such that Fraunhofer geometry applies. The light on the screen is known as the diffraction pattern.

$https://www.doitpoms.ac.uk/tlplib/diffraction/images/diffraction.jpg$

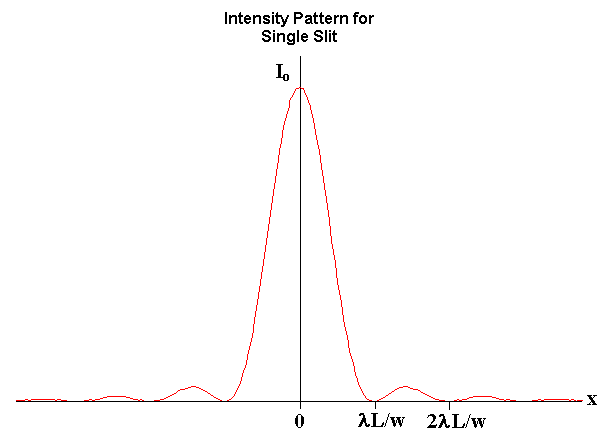
The form of the diffraction pattern from a single slit mask, of width w, involves the mathematical “sinc function”, where

$\operatorname{sinc}(z)=\frac{\sin (z)}{z}$

The observable pattern projected onto the screen (a distance L away) has an intensity pattern as follows, where x is the distance from the straight-through position:

$I(x)=I_{o} \operatorname{sinc}^{2}\left(\frac{\pi x w}{\lambda L}\right)$

Schematic diagram of slit and screen with dimensions marked

Note that sinc(0) = 1.

Graph showing intensity pattern for a single slit

Diffraction patterns can be calculated mathematically. The operation that directly predicts the amplitude of the diffraction pattern from the mask is known as a Fourier Transform (provided the conditions for Fraunhofer Diffraction are satisfied). The derivation of some simple patterns can be found here.

$https://www.doitpoms.ac.uk/tlplib/diffraction/images/grating-a.jpg$	$https://www.doitpoms.ac.uk/tlplib/diffraction/images/grating-b.jpg$
(a) s = 12 μm	(b) s = 3 μm

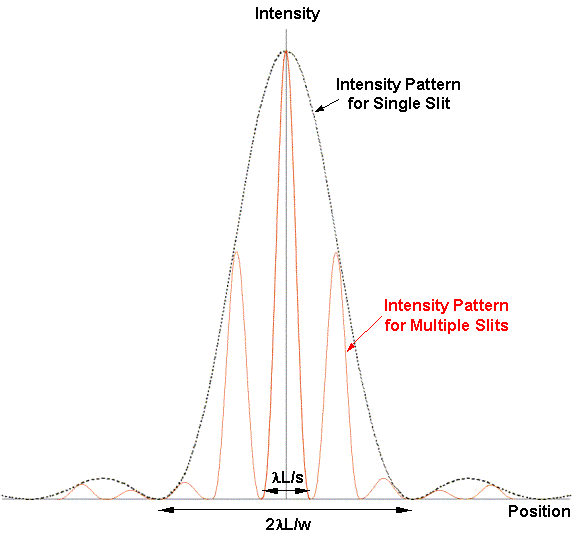
A diffraction grating is effectively a multitude of equally-spaced slits. The diffraction pattern from a complex mask such as a grating can be constructed from simplier patterns via the convolution theorem. The observed diffraction pattern is composed of repeated "sinc-squared" functions. Their positions from the central spot are determined by s (the spacing between slits) and their relative intensity is dependent on w (the width of individual slits).

$Diagram of diffraction grating labelled with slit spacing s and slit width w$

Slit spacing s and slit width w

$Graph showing intensity pattern from a diffraction grating$

$https://www.doitpoms.ac.uk/tlplib/diffraction/images/gratings-dp.jpg$

Diffraction patterns from gratings (a) and (b).

By considering diffraction from a grating, the reciprocal nature of the pattern can be derived. This relationship can be seen in the diffraction patterns of the slits: small features of the diffracting object give wide spacings in the diffraction pattern

$s=\frac{\lambda L}{x}$

$https://www.doitpoms.ac.uk/tlplib/diffraction/images/slits-dp.jpg$

Diffraction patterns from slits of different widths.

More complicated masks, for example a periodic row of apertures, will show more intricate diffraction patterns, but still follow the same basic inverse relationship.

$Diagram of mask consisting of periodic row of apertures and resulting diffraction pattern$

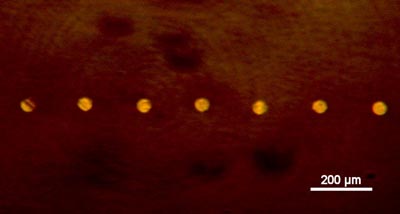
$Photograph of diffraction grating consisting of periodic row of apertures$

Mask consisting of periodic row of apertures

Diffraction pattern for periodic row of apertures

Support Center

How can we help?