17.2: Overdetermined Systems

Let us consider an overdetermined linear system - such as the one arising from the regression example earlier - of the form \[B z=g,\] or, more explicitly, \[\left(\begin{array}{ll} B_{11} & B_{12} \\ B_{21} & B_{22} \\ B_{31} & B_{32} \end{array}\right)\left(\begin{array}{l} z_{1} \\ z_{2} \end{array}\right)=\left(\begin{array}{l} g_{1} \\ g_{2} \\ g_{3} \end{array}\right) .\] Our objective is to find \(z\) that makes the three-component vector equation true, i.e., find the solution to the linear system. In Chapter 16 , we considered the "forward problem" of matrixvector multiplication in which, given \(z\), we calculate \(g=B z\). We also briefly discussed the "inverse" problem in which given \(g\) we would like to find \(z\). But for \(m \neq n, B^{-1}\) does not exist; as discussed in the previous section, there may be no \(z\) that satisfies \(B z=g\). Thus, we will need to look for a \(z\) that satisfies the equation "closely" in the sense we must specify and interpret. This is the focus of this section. \({ }_{-}^{1}\)

\({ }^{1}\) Note later (in Unit V) we shall look at the ostensibly simpler case in which \(B\) is square and a solution \(z\) exists and is even unique. But, for many reasons, overdetermined systems are a nicer place to start.

Interpretation

Let us consider a row interpretation of the overdetermined system. Satisfying the linear system requires \[B_{i 1} z_{1}+B_{i 2} z_{2}=g_{i}, \quad i=1,2,3 .\] Note that each of these equations define a line in \(\mathbb{R}^{2}\). Thus, satisfying the three equations is equivalent to finding a point that is shared by all three lines, which in general is not possible, as we will demonstrate in an example.

Example 17.2.1 row interpretation of overdetermined system

Let us consider an overdetermined system \[\left(\begin{array}{cc} 1 & 2 \\ 2 & 1 \\ 2 & -3 \end{array}\right)\left(\begin{array}{l} z_{1} \\ z_{2} \end{array}\right)=\left(\begin{array}{c} 5 / 2 \\ 2 \\ -2 \end{array}\right)\] Using the row interpretation of the linear system, we see there are three linear equations to be satisfied. The set of points \(x=\left(x_{1}, x_{2}\right)\) that satisfies the first equation, \[1 \cdot x_{1}+2 \cdot x_{2}=\frac{5}{2},\] form a line \[L_{1}=\left\{\left(x_{1}, x_{2}\right): 1 \cdot x_{2}+2 \cdot x_{2}=5 / 2\right\}\] in the two dimensional space. Similarly, the sets of points that satisfy the second and third equations form lines described by \[\begin{aligned} &L_{2}=\left\{\left(x_{1}, x_{2}\right): 2 \cdot x_{1}+1 \cdot x_{2}=2\right\} \\ &L_{3}=\left\{\left(x_{1}, x_{2}\right): 2 \cdot x_{1}-3 \cdot x_{2}=-2\right\} . \end{aligned}\] These set of points in \(L_{1}, L_{2}\), and \(L_{3}\), or the lines, are shown in Figure 17.3(a).

The solution to the linear system must satisfy each of the three equations, i.e., belong to all three lines. This means that there must be an intersection of all three lines and, if it exists, the solution is the intersection. This linear system has the solution \[z=\left(\begin{array}{c} 1 / 2 \\ 1 \end{array}\right) .\] However, three lines intersecting in \(\mathbb{R}^{2}\) is a rare occurrence; in fact the right-hand side of the system was chosen carefully so that the system has a solution in this example. If we perturb either the matrix or the right-hand side of the system, it is likely that the three lines will no longer intersect.

A more typical overdetermined system is the following system, \[\left(\begin{array}{cc} 1 & 2 \\ 2 & 1 \\ 2 & -3 \end{array}\right)\left(\begin{array}{l} z_{1} \\ z_{2} \end{array}\right)=\left(\begin{array}{c} 0 \\ 2 \\ -4 \end{array}\right)\] Again, interpreting the matrix equation as a system of three linear equations, we can illustrate the set of points that satisfy each equation as a line in \(\mathbb{R}^{2}\) as shown in Figure 17.3(b). There is no solution to this overdetermined system, because there is no point \(\left(z_{1}, z_{2}\right)\) that belongs to all three lines, i.e., the three lines do not intersect at a point.

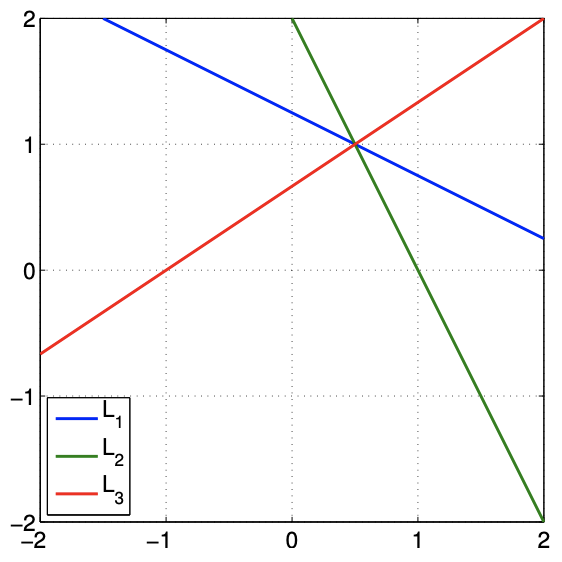
(a) system with a solution

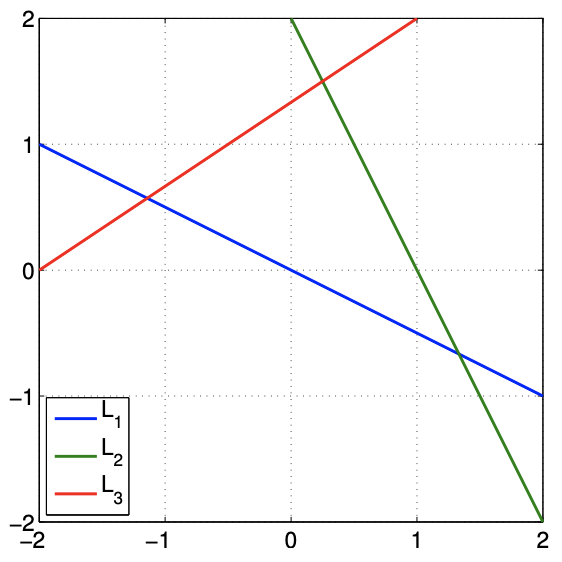
(b) system without a solution

Figure 17.3: Illustration of the row interpretation of the overdetermined systems. Each line is a set of points that satisfies \(B_{i} x=g_{i}, i=1,2,3\).

Column Interpretation

Let us now consider a column interpretation of the overdetermined system. Satisfying the linear system requires \[z_{1} \cdot\left(\begin{array}{l} B_{11} \\ B_{21} \\ B_{31} \end{array}\right)+z_{2} \cdot\left(\begin{array}{l} B_{12} \\ B_{22} \\ B_{32} \end{array}\right)=\left(\begin{array}{l} g_{1} \\ g_{2} \\ g_{3} \end{array}\right)\] In other words, we consider a linear combination of two vectors in \(\mathbb{R}^{3}\) and try to match the righthand side \(g \in \mathbb{R}^{3}\). The vectors span at most a plane in \(\mathbb{R}^{3}\), so there is no weight \(\left(z_{1}, z_{2}\right)\) that makes the equation hold unless the vector \(g\) happens to lie in the plane. To clarify the idea, let us consider a specific example.

Example 17.2.2 column interpretation of overdetermined system

\[\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right)\left(\begin{array}{c} z_{1} \\ z_{2} \end{array}\right)=\left(\begin{array}{c} 1 \\ 3 / 2 \\ 2 \end{array}\right)\] The column interpretation results in \[\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right) z_{1}+\left(\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right) z_{2}=\left(\begin{array}{c} 1 \\ 3 / 2 \\ 2 \end{array}\right)\] By changing \(z_{1}\) and \(z_{2}\), we can move in the plane \[\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right) z_{1}+\left(\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right) z_{2}=\left(\begin{array}{c} z_{1} \\ z_{2} \\ 0 \end{array}\right)\]

Figure 17.4: Illustration of the column interpretation of the overdetermined system.

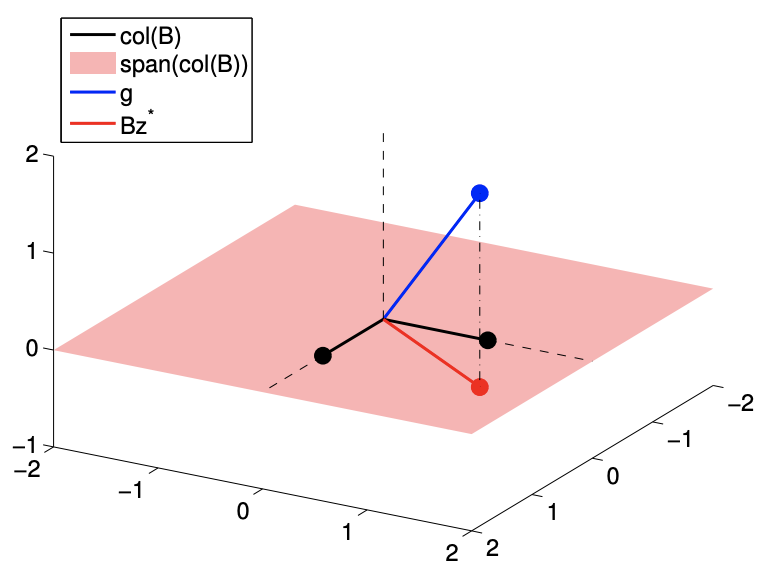
Clearly, if \(g_{3} \neq 0\), it is not possible to find \(z_{1}\) and \(z_{2}\) that satisfy the linear equation, \(B z=g\). In other words, \(g\) must lie in the plane spanned by the columns of \(B\), which is the \(1-2\) plane in this case.

Figure \(17.4\) illustrates the column interpretation of the overdetermined system. The vector \(g \in \mathbb{R}^{3}\) does not lie in the space spanned by the columns of \(B\), thus there is no solution to the system. However, if \(g_{3}\) is "small", then we can find a \(z^{*}\) such that \(B z^{*}\) is "close" to \(g\), i.e., a good approximation to \(g\). Such an approximation is shown in the figure, and the next section discusses how to find such an approximation.