6.2: Rotation and Viscous Effects

Last updated
Save as PDF

Page ID: 47253

Franz S. Hover & Michael S. Triantafyllou
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

In a fluid, unlike for rigid bodies, rotation angle is taken as the average of the angular deflections of the faces. Hence, a net rotation only occurs if the deflection of each face is additive. If they are opposing, then we have only a shearing of the element, with no rotation. Several cases are illustrated below for the two-dimensional case.

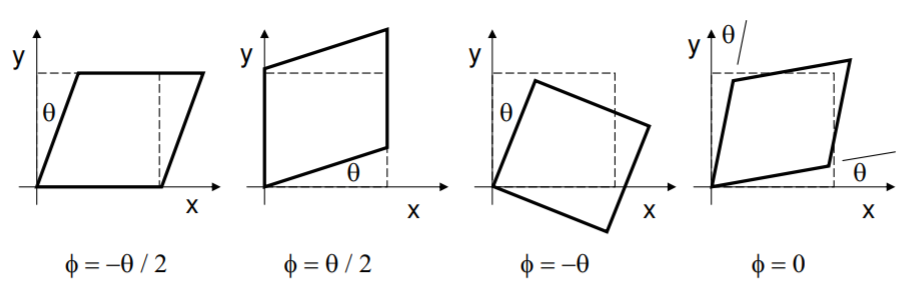Rotation of a two-dimensional form around different three-dimensional axes. — Figure \(\PageIndex{1}\): attempts at rotating a two-dimensional shape in three dimensions. Net rotation occurs in the 3 cases on the left but only a shearing, not a net rotation, occurs in the rightmost case.

Now the rotation rate in the \(z\) direction is \(\frac{\partial v}{\partial x}\) (the counterclockwise deflection rate of the horizontal face in the plots above), minus \(\frac{\partial u}{\partial y}\) (clockwise deflection rate of the vertical face in the plots above). Giving the three-dimensional rotation rate the vector symbol \(\vec{w}\), we have

\[ \vec{w} = \left[ \dfrac{\partial w}{\partial y} - \dfrac{\partial v}{\partial z} \quad \quad \dfrac{\partial u}{\partial z} - \dfrac{\partial w}{\partial x} \quad \quad \dfrac{\partial v}{\partial x} - \dfrac{\partial u}{\partial y} \right] ^T . \]

Despite this attention, we will now argue that rotational effects are negligible in large water waves. The center of the argument is the fact that a spherical particle will have no rotation except through shear forces. At the same time, however, the Reynolds number in ocean-scale waves has to be taken into account; it is the ratio of inertial to viscous forces

\[ Re = \dfrac{U d}{\nu}, \]

where the characteristic speed and length scales are \(U\) and \(d\) respectively, with \(\nu\) the kinematic viscosity \( (\mu \rho) \). The kinematic viscosity of water at typical ocean temperatures is \(1e - 6 m^2/s\). In contrast, velocities encountered in ocean waves are on the order of \(10 m/s\), with flow structures on the scale of meters or more. Hence the Reynolds number is very large, and the viscous forces may be neglected. This means in particular that \(\vec{w}\) is zero and that we will neglect all terms with \(\mu\) in the force balance.

Note that the inviscid and irrotational assumption is not necessarily valid near solid boundaries, where very small flow structures associated with turbulence result from the no-slip boundary condition.