Magnetostriction
- Page ID
- 335
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Magnetostriction is a property of ferromagnetic materials which causes them to expand or contract in response to a magnetic field. This effect allows magnetostrictive materials to convert electromagnetic energy into mechanical energy. As a magnetic field is applied to the material, its molecular dipoles and magnetic field boundaries rotate to align with the field. This causes the material to strain and elongate (Figure \(\PageIndex{1}\)).

As the applied magnetic field increases in intensity, the magnetostrictive strain on the material increases. Ferromagnetic materials that are isotropic and have few impurities are most effective in magnetostriction because these properties allow their molecular dipoles to rotate easily. Magnetostriction was first measured by James Prescott Joule (1818-1889) who was able to magnetize an iron sample and measure its the change in length. The opposite effect, in which an applied stress caused the material to create a magnetic field, was discovered by E. Villari (1836-1904). Gustav Wiedemann then discovered that a ferromagnetic rod would oscillate torsionally when exposed to a longitudinal and circular magnetic field.
Background
The interior of a ferromagnetic material is divided into magnetic “domains.”
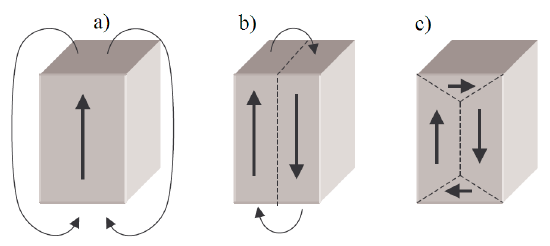
Within a domain, the molecules are aligned so that their dipoles point in the same direction. This causes a north and south pole or oppositely-charged portions on opposite sides of the domain. A material can have any number of domains as long as the number of domains minimizes the internal energy of the structure. The boundaries separating these regions (in bulk materials) are called Bloch walls. Bloch walls are made up of a thin layer of molecules in which their molecular dipoles are gradually rotated to align with their adjacent domains.
The orientation of a Bloch wall depends on the directions of the applied magnetic field and the magnetic anisotropy of the crystal structure. When a magnetic field is applied to a ferromagnetic material, the magnetic field applies a force on the material’s molecular dipoles which pushes them to align with the field. As the dipoles rotate, a strain is produced in the material, causing it to elongate (Figure \(\PageIndex{1}\)).
In addition to magnetic fields, the magnetic anisotropy of a material determines the preferred direction of molecular dipoles. For example, in a face centered cubic (FCC) unit cell, the dipoles prefer to align along the edge of the cube. This is called the “easy direction,” and this direction varies between different unit cell structures.
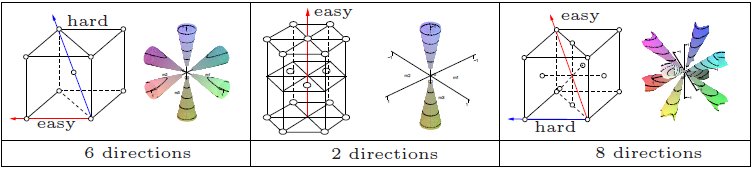
Additionally, magnetic anisotropy can be created by applying stress to the material. If a stress is applied, the direction of stress becomes preferred magnetic direction, and the Bloch walls will align with the stress. When a magnetic field is applied in a direction not parallel to the stress, the stress causes the dipoles to resist rotation to align with the magnetic field. For an applied magnetic field to reorient the molecular dipoles, it must overcome the material's crystal anisotropy force on the dipoles.
Bloch wall orientation also depends on impurities within the crystal structure, which inhibit the movement of Bloch walls. Because ferromagnetic materials have few impurities, their Bloch walls are easily rotated and changed. These properties make ferromagnetic materials ideal for magnetostriction.
Behavior
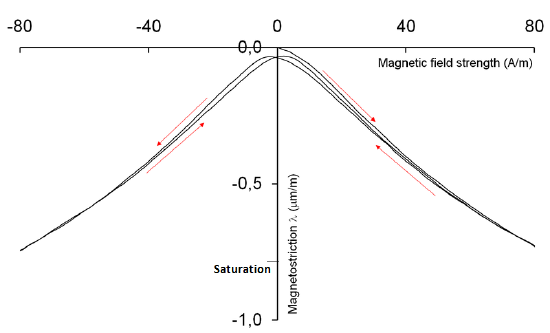
The degree of magnetostriction can be measured by the magnetostrictive coefficient λ, which is the ratio of the fractional change in length (also known as strain or the change in length divided by the original length) to the magnetization of the material. Between 0 A/m and the saturation magnetization, the relationship between the change in length and the magnetization is linear then decays as in the hysteresis loop in Figure \(\PageIndex{5}\). The magnetostrictive coefficient is the proportionality constant between these two values and is only applicable as magnetization increases to its saturation value.
Some magnetostriction coefficients for various materials can be seen below:
| Material | Crystal Axis |
Magnetostriction Coefficient λ (x10^-5) ((m/m)/(A/m)) |
|---|---|---|
| Fe | 100 | +(1.1-2.0) |
| Fe | 111 | -(1.3-2.0) |
| Fe | polycrystal | -0.8 |
| Ni | 100 | -(5.0-5.2) |
| Ni | 111 | -2.7 |
| Ni | polycrystal | -(2.5-4.7) |
| Co | polycrystal | -(5.0-6.0) |
These values represent the change in length to the magnetization of the material. In the table, iron and nickel show some anisotropy with respect to the preferred direction of the magnetic field. The values above were measured experimentally. (See reference 3)
The saturation magnetization is the point at which the material obtains maximum alignment with the applied magnetic field. This corresponds to the maximum magnetic moment that can be obtained. The magnetostrictive coefficient is only applicable until the saturation magnetization because the material reaches its maximum strain and cannot continue to elongate at this point. The maximum elongation also corresponds to a 90 degree Bloch wall and domain rotation over the total volume of material. In other words, the saturation magnetization varies between materials and occurs when their domains have all been aligned. Any increase of the applied magnetic field past the saturation point would then not affect the material because its domains could not be further aligned.
When the applied magnetic field is removed and no stress is applied to the material, the magnetostriction exhibits some hysteresis. This occurs because the material is still magnetized when the magnetic field is removed. which results in nonzero strain in the material. On the other hand, when no stress and no magnetic field is applied to the material, the preferred magnetic field direction is determined by the crystal anisotropy energy. When applying a stress and no magnetic field to the material, a strain is created in the material, which then creates magnetoelastic energy. This energy then contributes to the total magnetization of the material. Thus, the direction of the magnetic field created by the material is dependent on both the direction of the applied magnetic field and the anisotropy caused by strain and the crystal structure.
Applications
Magnetostrictive materials are used to convert electromagnetic energy into mechanical energy and vice versa. This effect can be used to create sensors that measure a magnetic field or detect a force. The magnetic field or force applied would create a strain in the material, which can be measured.
Transformers also use mangnetostrictive materials in conjunction with Faraday's law to convert magnetic fields into an electromotive force. During this process, the change in magnetic flux is converted into an electromotive force (EMF) in the transformer. This effect is used to increase or decrease AC voltages and to transfer them from one circuit to another. When exposed to a changing magnetic field (wave) the magnetostrictive material responds by rotating its molecular dipoles in phase with this frequency. The maximum change in length of the material occurs twice per period of the magnetic field. This results in a humming sound, which is commonly heard from transformers.
A changing magnetic field can also be used in conjunction with magnetostrictive materials to produce vibrations. Such materials are used in medical devices and industrial vibrators, ultrasonic cleaning devices, underwater sonar, vibration or noise control systems, and in many other applications. The amplitude of vibration can be increased using a mechanical lever. Similarly, magnetostrictive transducers can be used to transfer ultrasonic energy into other materials.
Questions
- For an AC transformer subject to a 60Hz applied magnetic field, what is the frequency of sound produced by the transformer?
- Name three factors influencing the direction of domains in a magnetostrictive material.
- What is the magnetization of a piece of iron that has a 1.5nm/mm strain in the 100 direction?
Answers
- For an AC transformer subject to a 60Hz applied magnetic field, what is the frequency of sound produced by the transformer?
- 120Hz. The maximum change in length occurs twice per period of the magnetic field, so the frequency produced by the transformer is twice the frequency of the magnetic field.
- Name three factors influencing the direction of domains in a magnetostrictive material.
- The direction of an applied magnetic field
- A crystal lattice structure creating magnetic anisotropy
- Impurities in the material
- What is the magnetization of a piece of iron that has a 1.5nm/mm strain in the 100 direction?
- The strain is 2*10^-6m/m. In the 100 direction for Fe, the magnetostrictive coefficient is (1.1-2.0)*10^-5 m/A per unit strain. Thus, the magnetization values are:
-
- The range of magnetization is 0.10-0.18 A/m.
Contributors and Attributions
- Gabrielle Yu (University of California, Davis, Fall 2015)

