Meissner Effect

Since its discovery in 1911 by Heike Kamerlingh Onnes, superconductivity has been an important area of research for physicists and engineers alike. Starting with the discovery of mercury as a superconducting material, the list of superconductors has grown to include more than just conductive metals, as many ceramics also exhibit superconducting properties. Although many metals are conductive, not all conducting materials are superconductive, and even some insulators are able to become superconductive under the right conditions. Superconductors have gained interest due to their ability to drop their resistivity to zero when the material is below a certain temperature. This critical temperature is the distinction defining how a superconductor behaves, since the properties of a superconductor are different above and below the critical temperature. One phenomena that occurs in superconductors below the critical temperature is the Meissner effect, which is where a superconductor expels all magnetic field from within itself. One of the most well known demonstrations of the Meissner effect is its ability to make a magnet levitate above a superconductor, as seen in Figure \(\PageIndex{1}\). The cause behind this phenomena is more complex than magnetic repulsion.

Figure \(\PageIndex{1}\): A magnet is able to levitate above a superconductor due to the Meissner effect. (CC BY-SA 3.0;  Peter nussbaumer via Wikipedia)

How it Works

Above the critical temperature, T_c, a superconductor has no notable effect when a magnetic field is applied, as the magnetic field is able to pass through the superconductor unhindered. If the superconductor is below its critical temperature, the applied magnetic field is expelled from the inside of the superconductor and bent around it, as seen in Figure \(\PageIndex{2}\). These magnetic fields are expelled because under the influence of a magnetic field, surface currents that flow without resistance develop to create magnetization within the superconductor. This magnetization is equal and opposite to the magnetic field, resulting in cancelling out the magnetic field everywhere within the superconductor. This results in the superconductor having a magnetic susceptibility of -1, meaning it exhibits perfect diamagnetism. While many materials exhibit some small amount of diamagnetism, superconductors are strongly diamagnetic. Since diamagnetics have a magnetization that opposes any applied magnetic field, the superconductor is repelled by the magnetic field. When a magnet is placed above a superconductor, this repelling force can be stronger than gravity, allowing the magnet to levitate above the superconductor. This is not an entirely stable configuration, giving the magnet the freedom to spin above the superconductor while it tries to orient its magnetic poles. If the magnetic field is removed or the superconductor raises above the critical temperature, the surface currents and magnetization disappear, and the magnet will no longer levitate.

Figure \(\PageIndex{2}\): A comparison between how a superconductor acts when it is above and below the critical temperature, T_c. Above the critical temperature, the magnetic field is allowed to pass through the superconductor. But when the superconductor is below the critical temperature, the magnetic field lines are bent around it. (CC BY-SA 3.0 Unported; Piotr Jaworski via Wikipedia)

Critical Temperature

The critical temperature is the temperature that marks the difference between superconducting and non-superconducting properties within a superconducting material. Above this temperature, the superconductor will behave normally. In the case of metals, the resistance will decrease with a drop in temperature, similar to non-superconducting metals. When the critical temperature is reached, the resistance suddenly drops to zero, and the material behaves as a superconductor. This temperature is not constant for all superconductors, but varies depending on the material, with some superconductors have a lower critical temperature than others. Those with a critical temperature above 30K are called high temperature superconductors, such as Y-Ba-Cu-O with a critical temperature of 90 K. High temperature superconductors are especially useful due to it being easier to achieve superconductance in these materials because they do not need to be cooled to such low temperatures.

Type I and Type II Superconductors

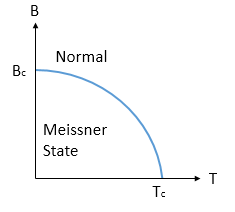
While superconductors may appear to react the same when in an applied magnetic field, there are differences that separate superconductors into two categories depending on how they react. For all superconductors, there is a maximum magnetic field, called the critical magnetic field, Bc, that can be applied before the magnetization opposing the magnetic field reaches a maximum and the superconductor reverts to its nonsuperconducting state. For a Type I superconductor, this direct relationship between the applied magnetic field and the opposing magnetization follows until the critical magnetic field is reached and superconduction no longer occurs. When this point is reached, the Meissner effect, which would occur within the superconductor up until the critical magnetic field, vanishes, and the magnetic field is able to pass through the superconductor unhindered. The range of the Meissner effect for a Type I superconductor can be seen in Figure \(\PageIndex{3}\).

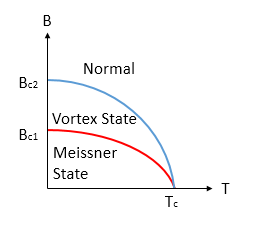
For Type II superconductors, there is an additional state that occurs between the Meissner state and the normal state. This state, called the mixed state or the vortex state, is noted by the mixing of the normal and Meissner states. The magnetic field is allowed to pass through the superconductor at specific parts where the normal state is occurring, while the rest of the superconductor exhibits the Meissner effect and expels the magnetic field. The shift from the Meissner effect to the vortex state occurs at a lower critical magnetic field, B_c1. This vortex state continues to occur to the upper critical magnetic field, B_c2, where the magnetic field becomes too strong for the superconductor to expel and the superconductor allows all magnetic fields to pass through it, returning it to its normal state. Between these two extremes the vortex state occurs, where small tubular regions develop within the superconductor, inside which the superconductor is in the normal state. The range of states for a Type II superconductor can be seen in Figure 4. Through these flux tubes or vortices, the magnetic field is allowed to pass. As with the edge of the superconductor, currents develop on the inside of the flux tubes, preventing the magnetic field from passing into the Meissner state sections of the superconductor. It is within this vortex state that flux pinning occurs.

Figure \(\PageIndex{4}\): The range of the different states for a Type II is superconducting, with the upper limits at the critical superconductor, with the Meissner state ranging from temperature, T_c, and the critical magnetic field, B_c. zero to the lower critical magnetic field, B_c1, and the Vortex state ranging from the lower critical magnetic field to the upper critical magnetic field, B_c2.

Flux Pinning

While the effects of flux pinning may appear similar to the levitating magnets caused by the Meissner effect, the cause behind flux pinning differs in some ways. For flux pinning to occur, the superconducting material either needs to be very thin or it needs to be a Type II superconductor. If it is thin or Type II, some of the magnetic field is allowed to pass through the superconductor, but only in specific spots, called flux tubes or a vortex. This passing of small amounts of the magnetic field through flux tubes can be seen in Figure \(\PageIndex{5}\). The reason the magnetic field is allowed to pass through the superconductor at these flux tubes is because there is no superconductivity within those regions. The superconductor tries to keep the flux tubes pinned to weaker parts of the superconductor, such as grain boundaries or other imperfections. When placed within a magnetic field, this pinning prevents the levitating superconductor from moving easily without an applied force, keeping it steady in a stable location. This is also known as quantum locking.

Figure \(\PageIndex{5}\): The internal view of a superconductor undergoing flux pinning, where the majority of the magnetic field lines can be seen bending around the superconductor, but some are allowed to pass through the superconductor, where they are concentrated at the flux tubes. (CC BY-SA 3.0; via Wikipedia)

Questions

1. What is the magnetic susceptibility of a superconductor and what kind of magnetism does it have?
2. What is the difference between Type I and Type II superconductors?
3. How does flux pinning differ from the Meissner effect?

Answers

1. The magnetic susceptibility equals -1, meaning the superconductor has perfect diamagnetism.
2. A Type I superconductor has the Meissner state before the magnetic field is raised too high and it reverts to the normal state while a Type II superconductor has an intermediate state between the Meissner and normal states called the vortex state.
3. Flux pinning allows magnetic field to pass through the superconductor in certain spots, or flux tubes, while the Meissner effect completely expels the magnetic field from the superconductor.

References

1. A. Z. Jones. "What is Quantum Levitation (and How Does it Work?)." Internet: physics.about.com/od/quantump...Levitation.htm.
2. S. O. Kasap. Principles of Electronic Materials and Devices. New York: McGraw Hill, 2006, pp. 729-736.
3. "Superconductivity: The Meissner Effect, Persistent Currents and the Josephson Effects." MIT Department of Physics, Feb. 8, 2011.

Contributors and Attributions

• Alicia Diebner, Materials Science and Engineering, University of California, Davis